Portfolio Optimization
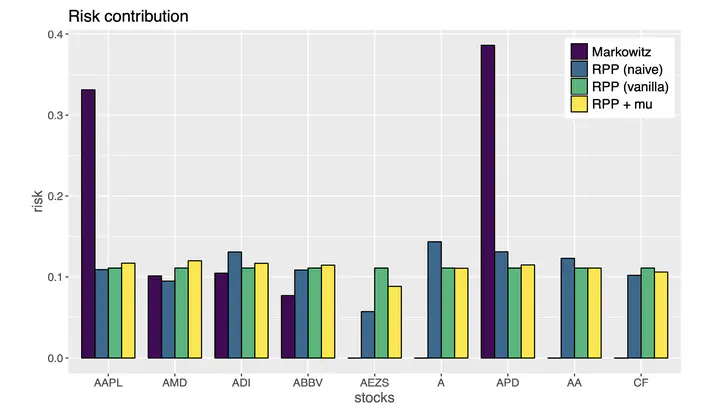 Risk parity portfolio
Risk parity portfolio
Portfolio optimization stands as a cornerstone of modern investment management, focusing on the systematic selection of optimal asset allocations that balance expected returns against financial risk. Since Harry Markowitz’s groundbreaking 1952 paper on Portfolio Selection, for which he later received the Nobel Prize in Economic Sciences, the field has evolved significantly beyond the traditional mean-variance framework. While the fundamental principle of optimizing portfolios based on the dual objectives of maximizing returns and minimizing risk remains central, practitioners have developed sophisticated approaches that account for real-world complexities such as transaction costs, market volatility, and diverse investment constraints. Modern portfolio optimization encompasses various methodologies, from robust optimization and alternative risk measures to factor models and machine learning approaches, all aimed at creating more resilient and efficient investment strategies that can adapt to changing market conditions and investor preferences.
Software
-
Portfolio Optimization
- riskParityPortfolio: Design of Risk Parity Portfolios [CRAN] - Listed in Task View on Empirical Finance
- riskparity.py: SCRIP: Successive Convex Optimization Methods for Risk Parity Portfolio Design (IEEE TSP 2015)
- highOrderPortfolios: Design of High-Order Portfolios via Mean, Variance, Skewness, and Kurtosis [CRAN]
- portfolioBacktest: Automated Backtesting of Portfolios over Multiple Datasets [CRAN]
- sparseIndexTracking: Design of Portfolio of Stocks to Track an Index [CRAN]
-
Financial Data Modeling
- intradayModel: Modeling and Forecasting Financial Intraday Signals [CRAN]
- fitHeavyTail: Mean and Covariance Matrix Estimation under Heavy Tails [CRAN]
- imputeFin: Imputation of Financial Time Series with Missing Values [CRAN] - Listed in Task View on Missing Data
- sparseEigen: Computation of Sparse Eigenvectors of a Matrix [CRAN]
Books
- Daniel P. Palomar, Portfolio Optimization: From Theory to Practive, Cambridge University Press, 2024.

-
Konstantinos Benidis, Yiyong Feng, and Daniel P. Palomar, Optimization Methods for Financial Index Tracking: From Theory to Practice, Foundations and Trends® in Optimization, Now Publishers, 2018. [pdf]

-
Yiyong Feng and Daniel P. Palomar, A Signal Processing Perspective on Financial Engineering, Foundations and Trends® in Signal Processing, Now Publishers, 2016. [pdf]
Papers
-
Runhao Shi and Daniel P. Palomar, “SAOFTRL: A Novel Adaptive Algorithmic Framework for Enhancing Online Portfolio Selection,” IEEE Trans. on Signal Processing, vol. –, pp. -, 2024.
-
Runhao Shi, Jiaxi Ying, and and Daniel P. Palomar, “Adaptive Passive-Aggressive Framework for Online Regression with Side Information,” Advances in Neural Information Processing Systems (NeurIPS), Vancouver, Canada, Dec. 2024. [25.8% acceptance rate]
-
Xiwen Wang, Rui Zhou, Jiaxi Ying, and Daniel P. Palomar, “Efficient and Scalable Parametric High-Order Portfolios Design via the Skew-t Distribution,” IEEE Trans. on Signal Processing, vol. 71, pp. 3726-3740, 2023.
-
Esa Ollila, Daniel P. Palomar, and Frédéric Pascal, “Affine equivariant Tyler’s M-estimator applied to tail parameter learning of elliptical distributions,” IEEE Signal Processing Letters, vol. 30, pp. 1017-1021, Aug. 2023.
-
Shengjie Xiu, Xiwen Wang, and Daniel P. Palomar, “A Fast Successive QP Algorithm for General Mean-Variance Portfolio Optimization,” IEEE Trans. on Signal Processing, vol. 71, pp. 2713-2727, July 2023.
-
Rui Zhou and Daniel P. Palomar, “Solving High-Order Portfolios via Successive Convex Approximation Algorithms,” IEEE Trans. on Signal Processing, vol. 69, pp. 892-904, Feb. 2021.
-
Esa Ollila, Daniel P. Palomar, and Frédéric Pascal, “Shrinking the Eigenvalues of M-estimators of Covariance Matrix,” IEEE Trans. on Signal Processing, vol. 69, pp. 256-269, Jan. 2021.
-
Rui Zhou, Junyan Liu, Sandeep Kumar, and Daniel P. Palomar, “Student’s t VAR Modeling with Missing Data via Stochastic EM and Gibbs Sampling,” IEEE Trans. on Signal Processing, vol. 68, pp. 6198-6211, Oct. 2020.
-
Rui Zhou and Daniel P. Palomar, “Understanding the Quintile Portfolio,” IEEE Trans. on Signal Processing, vol. 68, pp. 4030-4040, July 2020.
-
Linlong Wu, Yiyong Feng, and Daniel P. Palomar, “General Sparse Risk Parity Portfolio Design via Successive Convex Optimization,” Signal Processing, vol. 170, pp. 1-13, Dec. 2019.
-
Junyan Liu and Daniel P. Palomar, “Regularized Robust Estimation of Mean and Covariance Matrix for Incomplete Data,” Signal Processing, vol. 165, pp. 278-291, July 2019.
-
Junyan Liu, Sandeep Kumar, and Daniel P. Palomar, “Parameter Estimation of Heavy-Tailed AR Model With Missing Data Via Stochastic EM,” IEEE Trans. Signal Processing, vol. 67, no. 8, pp. 2159-2172, April 2019. [R package imputeFin]
-
Ziping Zhao, Rui Zhou, and Daniel P. Palomar, “Optimal Mean-Reverting Portfolio With Leverage Constraint for Statistical Arbitrage in Finance,” IEEE Trans. on Signal Processing, vol. 67, no. 7, pp. 1681-1695, April 2019.
-
Licheng Zhao and Daniel P. Palomar, “A Markowitz Portfolio Approach to Options Trading,” IEEE Trans. on Signal Processing, vol. 66, no. 16, pp. 4223-4238, Aug. 2018.
-
Ziping Zhao and Daniel P. Palomar, “Mean-Reverting Portfolio With Budget Constraint,” IEEE Trans. on Signal Processing, vol. 66, no. 9, pp. 2342-2357, May 2018.
-
Konstantinos Benidis, Yiyong Feng, and Daniel P. Palomar, “Sparse Portfolios for High-Dimensional Financial Index Tracking,” IEEE Trans. on Signal Processing, vol. 66, no. 1, pp. 155-170, Jan. 2018. [R package sparseIndexTracking]
-
Ying Sun, Prabhu Babu, and Daniel P. Palomar, “Robust Estimation of Structured Covariance Matrix for Heavy-Tailed Elliptical Distributions,” IEEE Trans. on Signal Processing, vol. 64, no. 14, pp. 3576-3590, July 2016. [Matlab code]
-
Yiyong Feng and Daniel P. Palomar, “SCRIP: Successive Convex Optimization Methods for Risk Parity Portfolio Design,” IEEE Trans. on Signal Processing, vol. 63, no. 19, pp. 5285-5300, Oct. 2015. [R package riskParityPortfolio]
-
Ying Sun, Prabhu Babu, and Daniel P. Palomar, “Regularized Robust Estimation of Mean and Covariance Matrix Under Heavy-Tailed Distributions,” IEEE Trans. on Signal Processing, vol. 63, no. 12, pp. 3096-3109, June 2015. [Matlab code] [R package fitHeavyTail]
-
Junxiao Song, Prabhu Babu, and Daniel P. Palomar, “Sparse Generalized Eigenvalue Problem via Smooth Optimization,” IEEE Trans. on Signal Processing, vol. 63, no. 7, pp. 1627-1642, April 2015. [Matlab code]
-
Yiyong Feng, Daniel P. Palomar, and Francisco Rubio, “Robust Optimization of Order Execution,” IEEE Trans. on Signal Processing, vol. 63, no. 4, pp. 907-920, Feb. 2015.
-
Yang Yang, Francisco Rubio, Gesualdo Scutari, and Daniel P. Palomar, “Multi-Portfolio Optimization: A Potential Game Approach,” IEEE Trans. on Signal Processing, vol. 61, no. 22, pp. 5590-5602, Nov. 2013.
-
Mengyi Zhang, Francisco Rubio, Daniel P. Palomar, and Xavier Mestre, “Finite-Sample Linear Filter Optimization in Wireless Communications and Financial Systems,” IEEE Trans. on Signal Processing, vol. 61, no. 20, pp. 5014-5025, Oct. 2013.
-
Mengyi Zhang, Francisco Rubio, and Daniel P. Palomar, “Improved Calibration of High-Dimensional Precision Matrices,” IEEE Trans. on Signal Processing, vol. 61, no. 6, pp. 1509-1519, March 2013.
-
Francisco Rubio, Xavier Mestre, and Daniel P. Palomar, “Performance Analysis and Optimal Selection of Large Minimum-Variance Portfolios under Estimation Risk,” IEEE Journal on Selected Topics in Signal Processing: Special Issue on Signal Processing Methods in Finance and Electronic Trading, vol. 6, no. 4, pp. 337-350, Aug. 2012.