Research Topics

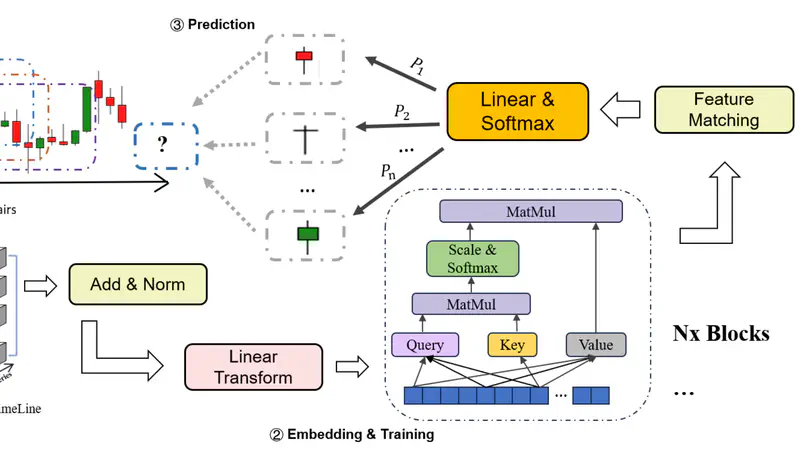
Deep learning has emerged as a powerful tool for analyzing high-frequency financial data, offering sophisticated capabilities to capture complex patterns and nonlinear relationships in market dynamics. These advanced models, particularly those based on Transformer networks, recurrent neural networks (RNNs), and long short-term memory (LSTM) networks, can process massive amounts of time-series data to predict market movements, assess volatility, and automate trading decisions with remarkable precision.

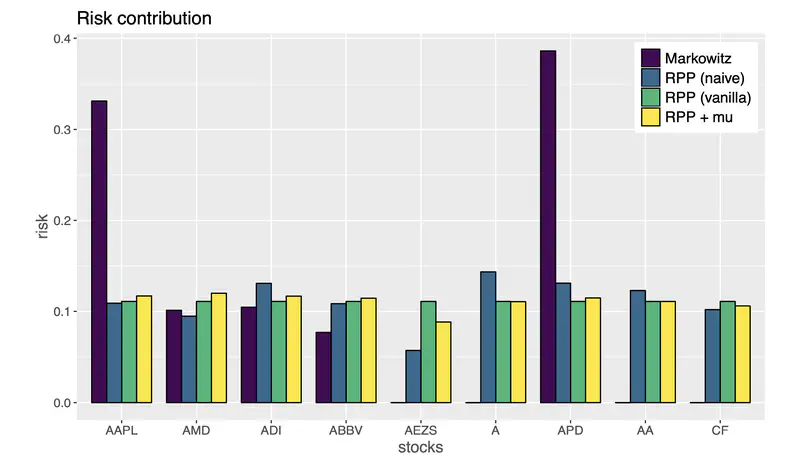
Portfolio optimization stands as a cornerstone of modern investment management, focusing on the systematic selection of optimal asset allocations that balance expected returns against financial risk. Since Harry Markowitz’s groundbreaking 1952 paper on Portfolio Selection, for which he later received the Nobel Prize in Economic Sciences, the field has evolved significantly beyond the traditional mean-variance framework.

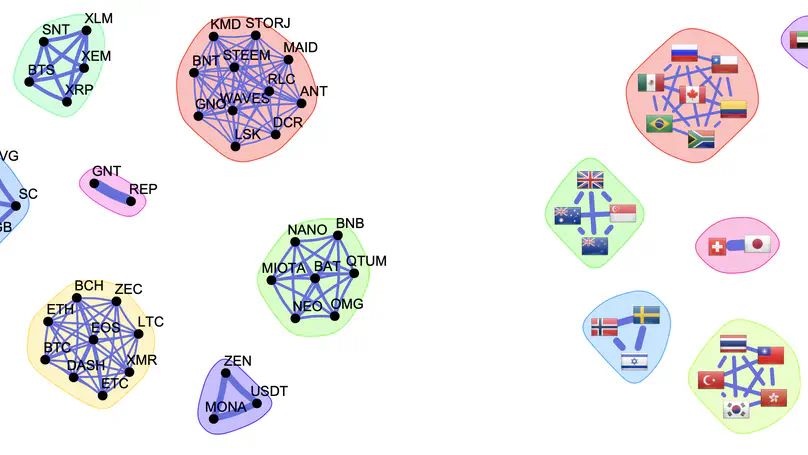
Financial markets are inherently interconnected systems where assets, institutions, and market participants form complex networks of relationships that evolve over time. Graph learning has emerged as a powerful framework for understanding and modeling these financial networks, enabling the discovery of meaningful relationships among stocks, cryptocurrencies, or other financial instruments through their return time series, trading volumes, or other market indicators.

Signal processing and financial engineering are seemingly different areas that share strong connections underneath. Both areas rely on the statistical analysis and modeling of systems and signals, either from the financial markets or from communication channels.

Traditional convex optimization methods and signal processing techniques can be employed in big data problems characterized by large amounts of data in high-dimensional spaces. However, big data brings additional difficulties that need to be taken care of such as high-computational cost that require simple and efficient methods, distributed implementations, faulty data in the form of outliers, etc.

The design of communication systems depends strongly on the degree of knowledge of the channel state information (CSI). The best spectral efficiency and/or performance is obviously achieved when perfect CSI is available at both sides of the link.

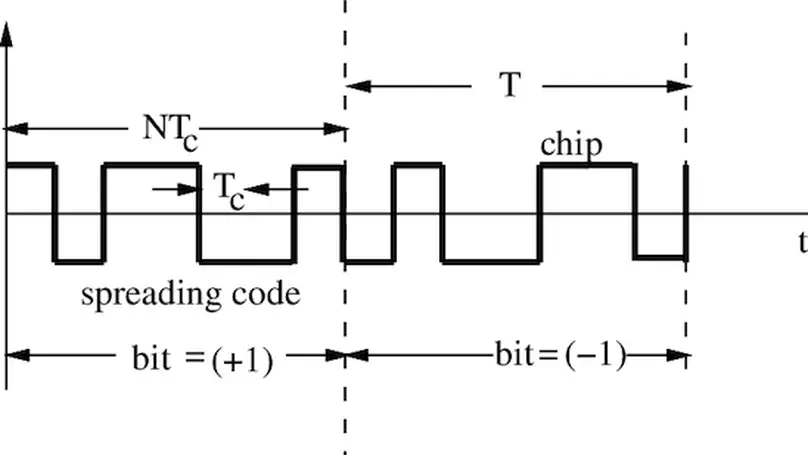
Carefully designed sequences lie at the heart of virtually any digital system commonly used in our daily lives. Examples include GPS synchronization, multiuser CDMA systems, radar ambiguity function shaping, cryptography for secure transactions, and even the watermarking of digital images or videos.

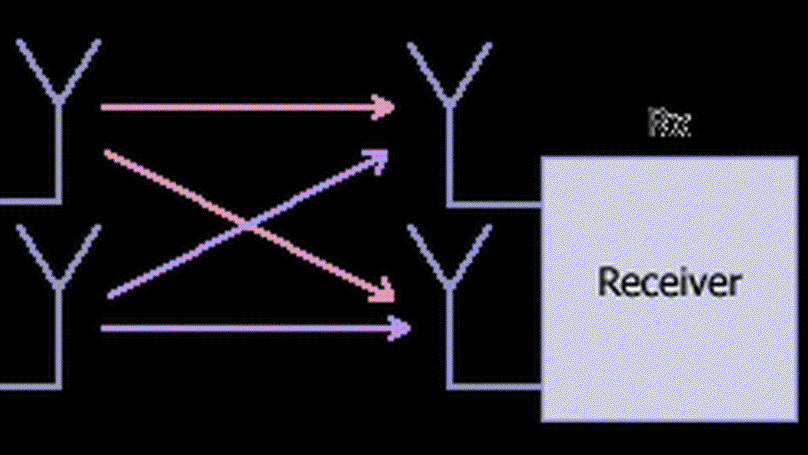
Multiple-input multiple-output (MIMO) channels provide an abstract and unified representation of different physical communication systems, ranging from multi-antenna wireless channels to wireless digital subscriber line systems. They have the key property that several data streams can be simultaneously established.

Semidefinite programming (SDP) is a class of convex optimization problems with a rich theory that can be efficiently solved in polynomial time. Many problems in wireless communications and radar systems can be formulated as SDPs with additional rank constraints.

The Variation Inequality (VI) problem constitutes a very general class of problems in nonlinear analysis. The VI framework embraces many different types of problems such as systems of equations, optimization problems, equilibrium programming, complementary problems, saddle-point problems, Nash equilibrium problems, and generalized Nash equilibrium problems.

Radio regulatory bodies are recently recognizing that rigid spectrum assignment granting exclusive use to licensed services is highly inefficient. A more efficient way to utilize the scarce spectrum resources is with a dynamic spectrum access, depending on the real spectrum usage and traffic demands.

Information theory and estimation theory have generally been regarded as two separate theories with little overlap. Recently, however, it has been recognized that the relations between the two theories are fundamental (e.

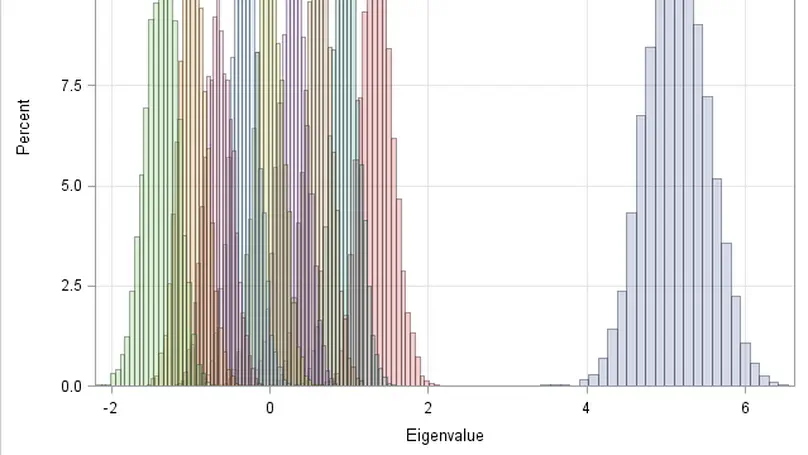
The performance of multiple-input multiple-output (MIMO) communication systems is related to the eigenstructure of the channel matrix H (channel eigenmodes) or, more exactly, to the non-zero eigenvalues of HH†. Therefore, the probabilistic characterization of these eigenvalues is necessary in order to derive analytical expressions for the average and outage performance measures of the system.

The use of complex numbers allows for a compact notation in many areas such as in baseband representation of communication systems. Quaternions constitute a further step: they are four-dimensional hypercomplex numbers.

During the last decade, it has been widely recognized that an independent optimization of the different OSI layers in a communication system is a limiting design factor. Instead, a cross-layer design is necessary.

Many communication systems of interest contain multiple uncoordinated users that share a common medium (e.g., wireless ad-hoc networks). These systems can be mathematically modeled as the so-called interference channel, for which the capacity region is still unknown.

Beamforming in wireless communication systems with multiple receive antennas has been studied for the last three decades. Traditionally, the design of the beamformer is based on either the knowledge of the spatial signature of the signal of interest or the availability of a training sequence.